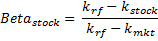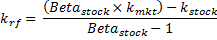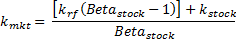Capital Asset Pricing Model (CAPM)

The Capital Asset Pricing Model is used to calculate a stock's necessary rate of return as a function of its volatility and the market's relative risk and rate of return.

The Capital Asset Pricing Model (CAPM) is used to calculate a security's current expected return. This model implies that every stock moves in some way related to the market in general and that the necessary rate of return for every stock can be derived by knowing this relationship, as well as the required rate of return for the market and the lowest required risk-free rate of return. To solve the calculation, use the capital asset pricing model calculator below.

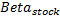• A stock's volatility in comparison to the market.
• The market's rate of return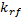
• The return on a risk-free investment
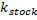• Investors' necessary rate of return on a stock.

Capital Asset Pricing Model Formula

• 
• 
• 
• 

What is the Capital Asset Pricing Model (CAPM)?

The CAPM Capital Asset Pricing Model is a mathematical model that attempts to explain how capital assets are priced in the market. The essential assumptions of this model provide information on how it operates. Investors want to earn a return on their money by investing in assets with a high projected rate of return. Investors put their money at risk when they invest in these funds.

Investors will balance expected rates of return with expected levels of risk when determining which asset to invest in. This means that all else being equal, investors will choose the asset with the highest expected rate of return and the lowest amount of risk feasible.

The "market" is made up of all conceivable stocks and represents the sum of their returns and risk levels. When we talk about risk in capital assets, we truly mean volatility. The change in the value of an asset, how much the price grows or lowers, is referred to as volatility. A high degree of volatility indicates that a certain asset (stock) will fluctuate in price more than another asset with lower volatility.

The CAPM Capital Asset Pricing Model argues that the volatility of any single asset can be connected to market volatility as a whole. Beta is the link between the price of a single asset and the market value. When the market rises, an asset with a high Beta will rise in price more than the market, and fall in price more than the market. When the market moves, a Beta of 1 is expected to move to the same degree as the market, a Beta of less than 1 is expected to move to a lesser degree than the market, and a Beta of greater than 1 is expected to move to a bigger degree than the market. There is even the possibility of having a negative Beta. A negative Beta indicates that the asset's price tends to fall as the market's value rises. The bigger the value of the negative Beta, as with the positive Beta, indicates the degree to which the asset varies inversely to the market.

According to the CAPM Capital Asset Pricing Model, this is the primary determinant of asset prices in the market. This idea is followed by other models, such as the Gordon Model (Constant Dividend Growth), which argues that price can be determined by an investor's rate of return.

What is the Risk-Free Rate of Return?

In the CAPM Capital Asset Pricing Model, the risk-free rate of return refers to the rate of return an investor can earn without exposing their funds to any risk. This interest rate, which is often based on the rate paid on short-term federal treasury bills, serves as the foundation for the needed rate of return on all assets.

The risk-free rate of return will be included in the required rate of return regardless of the capital asset. Any return above the risk-free rate is due to the risk premium required by investors to accept a higher level of risk in their portfolio.

What is the Risk Premium?

The CAPM Capital Asset Pricing Model relies heavily on the risk premium. The risk premium is the primary determinant of the needed rate of return. Investors have a wide range of financial assets to choose from, which comprise the market as a whole. If an investor invested in the entire market, their necessary rate of return would be the rate of return on investment that the entire market provides. The risk premium is the difference between this rate of return and the risk-free rate.

Because the volatility of each asset may be compared to the volatility of the market, their risk premium will adjust to the same degree. Because the total required rate of return is the sum of the risk-free rate plus the risk premium, the variation in the total required rate of return is greater for high-risk assets than low-risk assets.

What is the necessary rate of return?

The necessary rate of return is just the sum of the risk-free and risk-premium rates. Each market asset will have a needed rate of return, which can be used to calculate the item's price. Because the volatility of each asset in the market changes, the required rate of return is constantly relative to the market rate of return.

What is Beta?

The idea of beta is significant in the CAPM Capital Asset Pricing Model because it defines the risk premium of any one asset about the risk of the market as a whole. Beta is a direct correlation of volatility between the entire market and any single asset. If an asset grows at a pace that is 200% of that of the market, the Beta of that asset is 2. A simple notion that demonstrates the value that investors place on risk and the premium that they require to accept it.

How is the CAPM Capital Asset Pricing Model calculated?

The CAPM Capital Asset Pricing Model is fairly simple to calculate. The above CAPM Capital Asset Pricing Model Calculator can be used to calculate the needed rate of return for any asset. The CAPM Capital Asset Pricing Model formula is as follows, with each version presented above beside the CAM Capital Asset Pricing Model Calculator.

The CAPM Capital Asset Pricing Model Formula

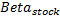• The relative volatility of a stock relative to the market
• The rate of return of the market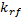
• The risk-free rate of return
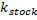• The required rate of return for a stock by investors
•